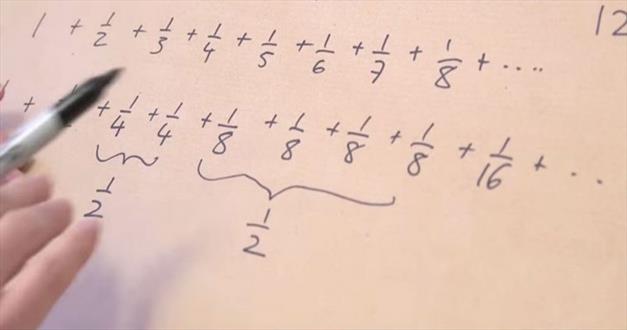از عدد مرموز دنیای ریاضی(۰.۵۷۷) و خواص جالب آن چه می دانید؟
اگر درباره اعداد عجیب و غریب و پر کاربرد و معروف دنیا از شما سوال کنند، احتمالا اولین عددی که به ذهنتان می رسد، عدد “پی” است. اما علاوه بر عدد پی، تقریبا در همه جا رد پایی از عدد جالب و عجیب ۰٫۵۷۷ نیز به چشم می خورد.
به گزارش پاپایا، علی رغم دانش و درک ما نسبت به دایره ها، عدد پی عددی نیست که به سادگی بتوان از آن استفاده کرد. چرا که مشخص کردن دقیق این عدد، تقریبا غیر ممکن است و بدون آن که بتوانیم هیچ الگوی خاصی را در ترتیب رقم های این عدد دوست داشتنی پیدا کنیم، محاسبه ارقام آن تا بی نهایت ادامه پیدا می کند.
با وجود طبیعت پیچیده خود، عدد پی به این علت معروف شده است که در همه جا، اعم از طبیعت و ریاضیات به چشم می خورد، حتی در جاهایی که هیچ ارتباط مستقیم و وروشنی با دایره ها و اشکال دایره ای شکل وجود ندارد. اما عدد پی تنها عددی نیست که چنین ویژگی منحصر به فرد و ترسناکی دارد! به دلایلی، عدد ۰٫۵۷۷ هم در هر جا که چشم می اندازیم، حضور دارد.
این عدد که با دنباله اویلر و یا دنباله اویلر-ماسکرونی شناخته می شود، در واقع اختلاف حد بین دو دنباله ریاضی، یعنی لگاریتم طبیعی و سری هارمونیک را توصیف می کند.
سری هارمونیک یکی از سری اعداد بسیار معروف است که اگر اعداد را به صورت زیر با هم جمع ببندید، به آن خواهید رسید:
۱+۱/۲+۱/۳+۱/۴+…
همان طور که می دانید این سری تا بی نهایت ادامه پیدا می کند.
لگاریتم طبیعی خیلی پیچیده تر از سری هارمونیک است اما در توضیح دنباله اویلر می توان گفت که اگر اختلاف بین مقادیر لگاریتم طبیعی و سری هارمونیک را به دست آوریم، به یک دنباله متناهی خواهیم رسید به نام دنباله اویلر. این عدد همان ۰٫۵۷۷ است که سه جایگاه اعشاری دارد. این عدد هم مانند عدد پی می تواند تا بی نهایت، یعنی تا حدود ۱ میلیارد رقم، ادامه پیدا کند. اما نکته مهم در مورد عدد ۰٫۵۷۷ این است که آن چه که این عدد قادر به توضیح آن است، بسیار قابل تامل است.
تصور کنید که ی ک دایره با محیط یک متر دارید و یک مورچه را بالای این دایره قرار می دهید. حالا تصور کنید که این مورچه با سرعت یک سانتی متر در هر ثانیه، شروع به حرکت دور دایره می کند، و در حالی که مورچه در حال دور زدن است، شما به طور مداوم، محیط دایره را در هر ثانیه، یک متر بزرگ تر می کنید!
پس در هر ثانیه، مورچه یک سانتی متر بر روی محیط دایره جلو تر می رود اما شما در هر ثانیه یک متر به محیط دایره اضافه می کنید. هیچ راهی نیست تا این مورچه بتواند یک دور کامل به دور دایره بزند، درست است؟
اگر فکر می کنید که مورچه نمی تواند یک دور کامل بزند، کاملا در اشتباه هستید! این مورچه قادر است تا با همان سرعت ثابت یک سانتی متر در هر ثانیه، یک دور کامل بر روی محیط دایره فرضی بزند، حتی با وجود آن که شما به طور مرتب در حال اضافه کردن محیط دایره هستید! دلیل این واقعیت این است که وقتی محیط دایره را زیاد می کنید، فقط به مقدار فاصله پیش روی مورچه اضافه نمی شود، بلکه به مقداری از دایره که مورچه طی کرده هم اضافه کرده اید.
البته قطعا تا مورچه مورد نظر ما بتواند تمام محیط دایره را دور بزند، عمر خورشید تمام شده است! بنا بر این این جا داریم از یک سری اعداد صحبت می کنیم که به طرزی باور نکردنی به کندی رشد می کند!
این مورد به خودی خود هم جذاب و جالب است، با این حال، شاید دانستن این نکته حتی ترسناک تر باشد که دنباله اویلر فقط در توضیح این معمای متناقض به کار نمی رود بلکه به طور مطلق در همه انواع مسایل فیزیک، از جمله چندین معادله مکانیک کوانتوم هم خود را نشان می دهد. همچنین همین عدد ۰٫۵۷۷ است که برای یافتن ذره بنیادی موسوم به “ذره خدا” یا همان Higgs boson به کار می رود! هیچ کس هیچ توضیحی برای این عدد ندارد و بشر تا به امروز هیچ وقت فکر نمی کرد که اعداد بتوانند تا این حد معما گونه و عجیب به نظر برسند!
منبع: sciencealert
با وجود طبیعت پیچیده خود، عدد پی به این علت معروف شده است که در همه جا، اعم از طبیعت و ریاضیات به چشم می خورد، حتی در جاهایی که هیچ ارتباط مستقیم و وروشنی با دایره ها و اشکال دایره ای شکل وجود ندارد. اما عدد پی تنها عددی نیست که چنین ویژگی منحصر به فرد و ترسناکی دارد! به دلایلی، عدد ۰٫۵۷۷ هم در هر جا که چشم می اندازیم، حضور دارد.
این عدد که با دنباله اویلر و یا دنباله اویلر-ماسکرونی شناخته می شود، در واقع اختلاف حد بین دو دنباله ریاضی، یعنی لگاریتم طبیعی و سری هارمونیک را توصیف می کند.
سری هارمونیک یکی از سری اعداد بسیار معروف است که اگر اعداد را به صورت زیر با هم جمع ببندید، به آن خواهید رسید:
۱+۱/۲+۱/۳+۱/۴+…
همان طور که می دانید این سری تا بی نهایت ادامه پیدا می کند.
لگاریتم طبیعی خیلی پیچیده تر از سری هارمونیک است اما در توضیح دنباله اویلر می توان گفت که اگر اختلاف بین مقادیر لگاریتم طبیعی و سری هارمونیک را به دست آوریم، به یک دنباله متناهی خواهیم رسید به نام دنباله اویلر. این عدد همان ۰٫۵۷۷ است که سه جایگاه اعشاری دارد. این عدد هم مانند عدد پی می تواند تا بی نهایت، یعنی تا حدود ۱ میلیارد رقم، ادامه پیدا کند. اما نکته مهم در مورد عدد ۰٫۵۷۷ این است که آن چه که این عدد قادر به توضیح آن است، بسیار قابل تامل است.
تصور کنید که ی ک دایره با محیط یک متر دارید و یک مورچه را بالای این دایره قرار می دهید. حالا تصور کنید که این مورچه با سرعت یک سانتی متر در هر ثانیه، شروع به حرکت دور دایره می کند، و در حالی که مورچه در حال دور زدن است، شما به طور مداوم، محیط دایره را در هر ثانیه، یک متر بزرگ تر می کنید!
پس در هر ثانیه، مورچه یک سانتی متر بر روی محیط دایره جلو تر می رود اما شما در هر ثانیه یک متر به محیط دایره اضافه می کنید. هیچ راهی نیست تا این مورچه بتواند یک دور کامل به دور دایره بزند، درست است؟
اگر فکر می کنید که مورچه نمی تواند یک دور کامل بزند، کاملا در اشتباه هستید! این مورچه قادر است تا با همان سرعت ثابت یک سانتی متر در هر ثانیه، یک دور کامل بر روی محیط دایره فرضی بزند، حتی با وجود آن که شما به طور مرتب در حال اضافه کردن محیط دایره هستید! دلیل این واقعیت این است که وقتی محیط دایره را زیاد می کنید، فقط به مقدار فاصله پیش روی مورچه اضافه نمی شود، بلکه به مقداری از دایره که مورچه طی کرده هم اضافه کرده اید.
البته قطعا تا مورچه مورد نظر ما بتواند تمام محیط دایره را دور بزند، عمر خورشید تمام شده است! بنا بر این این جا داریم از یک سری اعداد صحبت می کنیم که به طرزی باور نکردنی به کندی رشد می کند!
این مورد به خودی خود هم جذاب و جالب است، با این حال، شاید دانستن این نکته حتی ترسناک تر باشد که دنباله اویلر فقط در توضیح این معمای متناقض به کار نمی رود بلکه به طور مطلق در همه انواع مسایل فیزیک، از جمله چندین معادله مکانیک کوانتوم هم خود را نشان می دهد. همچنین همین عدد ۰٫۵۷۷ است که برای یافتن ذره بنیادی موسوم به “ذره خدا” یا همان Higgs boson به کار می رود! هیچ کس هیچ توضیحی برای این عدد ندارد و بشر تا به امروز هیچ وقت فکر نمی کرد که اعداد بتوانند تا این حد معما گونه و عجیب به نظر برسند!
منبع: sciencealert
کد مطلب: 425452